Note
Go to the end to download the full example code
Dipole source solution¶
A simple example showing how to use pfsspy to compute the solution to a dipole source field.
import astropy.constants as const
import astropy.units as u
import matplotlib.patches as mpatch
import matplotlib.pyplot as plt
import numpy as np
import sunpy.map
from astropy.coordinates import SkyCoord
from astropy.time import Time
import pfsspy
import pfsspy.coords as coords
To start with we need to construct an input for the PFSS model. To do this, first set up a regular 2D grid in (phi, s), where s = cos(theta) and (phi, theta) are the standard spherical coordinate system angular coordinates. In this case the resolution is (360 x 180).
nphi = 360
ns = 180
phi = np.linspace(0, 2 * np.pi, nphi)
s = np.linspace(-1, 1, ns)
s, phi = np.meshgrid(s, phi)
Now we can take the grid and calculate the boundary condition magnetic field.
def dipole_Br(r, s):
return 2 * s / r**3
br = dipole_Br(1, s)
The PFSS solution is calculated on a regular 3D grid in (phi, s, rho), where rho = ln(r), and r is the standard spherical radial coordinate. We need to define the number of rho grid points, and the source surface radius.
nrho = 30
rss = 2.5
From the boundary condition, number of radial grid points, and source surface, we now construct an Input object that stores this information
header = pfsspy.utils.carr_cea_wcs_header(Time('2020-1-1'), br.shape)
input_map = sunpy.map.Map((br.T, header))
pfss_in = pfsspy.Input(input_map, nrho, rss)
Using the Input object, plot the input field
m = pfss_in.map
fig = plt.figure()
ax = plt.subplot(projection=m)
m.plot()
plt.colorbar()
ax.set_title('Input dipole field')
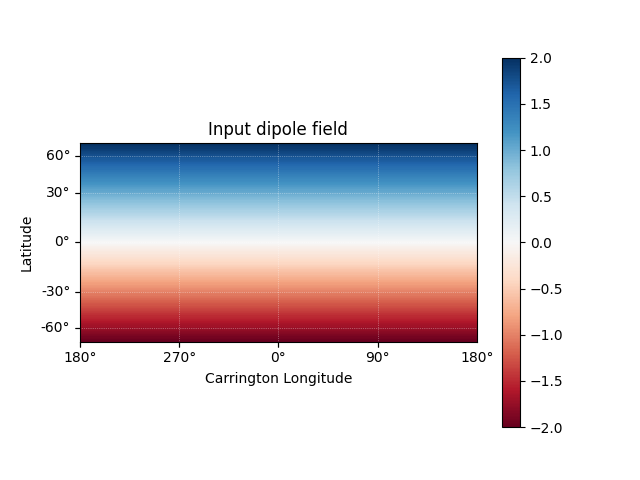
Text(0.5, 1.0, 'Input dipole field')
Now calculate the PFSS solution.
pfss_out = pfsspy.pfss(pfss_in)
Using the Output object we can plot the source surface field, and the polarity inversion line.
ss_br = pfss_out.source_surface_br
# Create the figure and axes
fig = plt.figure()
ax = plt.subplot(projection=ss_br)
# Plot the source surface map
ss_br.plot()
# Plot the polarity inversion line
ax.plot_coord(pfss_out.source_surface_pils[0])
# Plot formatting
plt.colorbar()
ax.set_title('Source surface magnetic field')
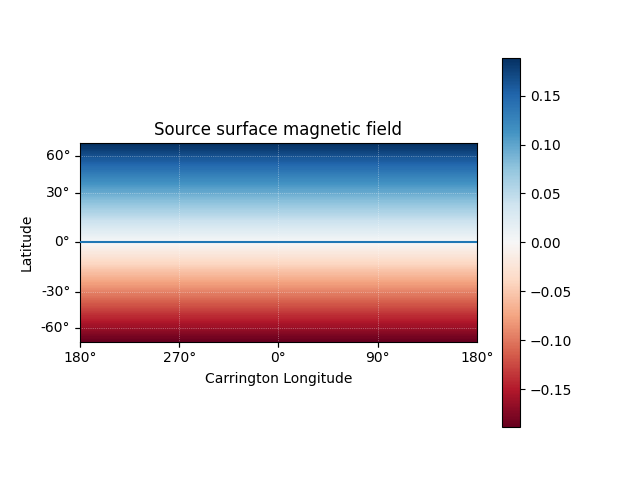
Text(0.5, 1.0, 'Source surface magnetic field')
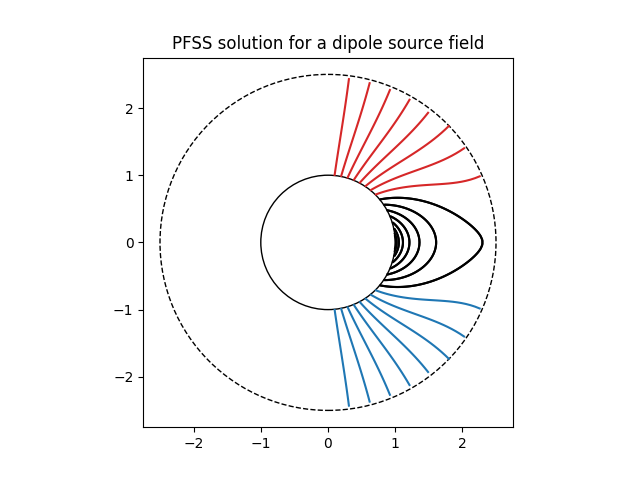
Finally, using the 3D magnetic field solution we can trace some field lines. In this case 32 points equally spaced in theta are chosen and traced from the source surface outwards.
fig, ax = plt.subplots()
ax.set_aspect('equal')
# Take 32 start points spaced equally in theta
r = 1.01 * const.R_sun
lon = np.pi / 2 * u.rad
lat = np.linspace(-np.pi / 2, np.pi / 2, 33) * u.rad
seeds = SkyCoord(lon, lat, r, frame=pfss_out.coordinate_frame)
tracer = pfsspy.tracing.FortranTracer()
field_lines = tracer.trace(seeds, pfss_out)
for field_line in field_lines:
coords = field_line.coords
coords.representation_type = 'cartesian'
color = {0: 'black', -1: 'tab:blue', 1: 'tab:red'}.get(field_line.polarity)
ax.plot(coords.y / const.R_sun,
coords.z / const.R_sun, color=color)
# Add inner and outer boundary circles
ax.add_patch(mpatch.Circle((0, 0), 1, color='k', fill=False))
ax.add_patch(mpatch.Circle((0, 0), pfss_in.grid.rss, color='k', linestyle='--',
fill=False))
ax.set_title('PFSS solution for a dipole source field')
plt.show()
Total running time of the script: (0 minutes 4.113 seconds)